TexSAW CTF 2025 - Writeups

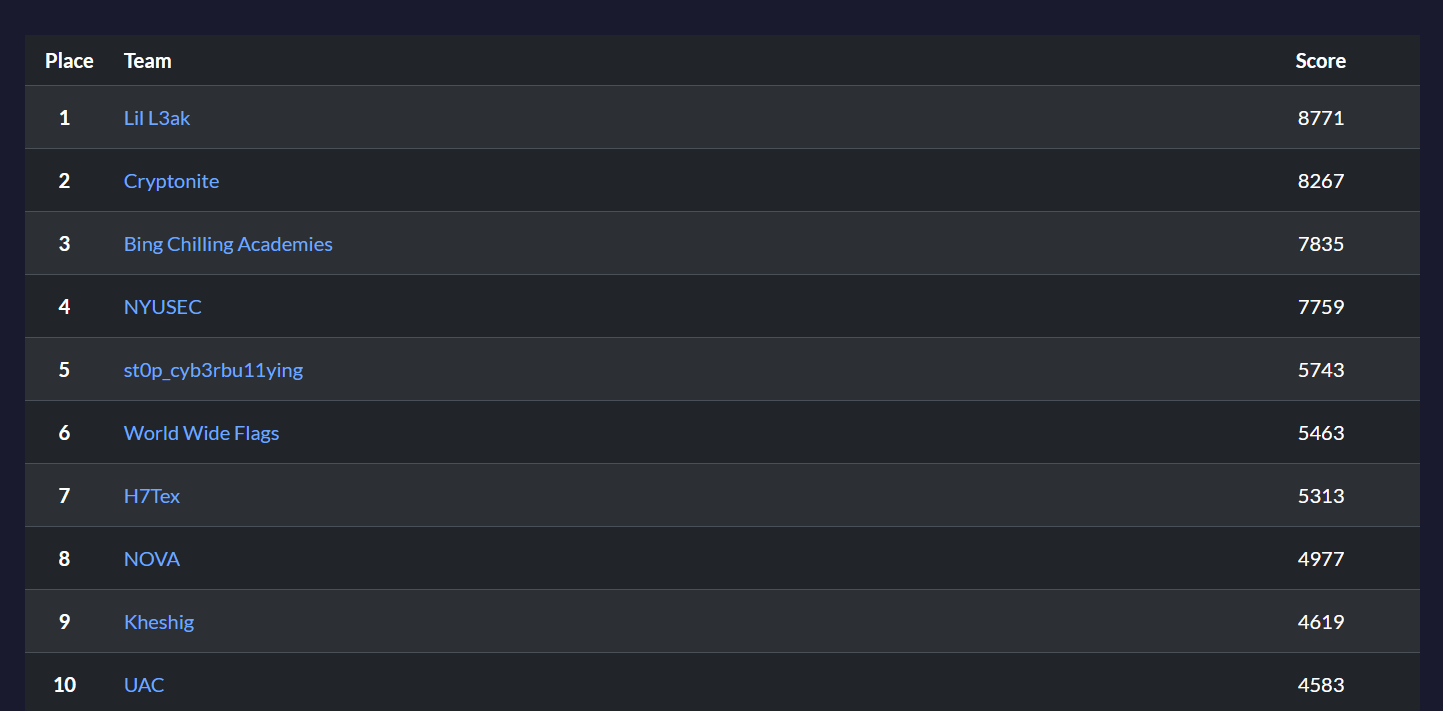
This is a writeup for some cryptography challenges I solved during TexSAW CTF 2025 as part of Lil L3ak. Very competitive ctf, but we secured 1st place!

Acknowledgements

Thanks to the TexSAW CTF team for organizing this event and providing us with these challenges. I had a lot of fun solving them.

Also, thanks to my teammates for their support and collaboration during the competition. Special thanks and kudos go to @abdelh and @___ts03___ for assisting with the cryptography challenges, @pk_0.6 for their astounding performance in the ctf, and @filipp1986, @vivig, @mideno and sk4r3kr0w for their overall contribution to the team. Special mention to @dre.cc for his amazing binary exploitation masterclass. Few out of many great teammates I had the pleasure to work with during this ctf.

Challenges

Venona [Crypto]

Description: You’ve been deployed on a classified reconnaissance mission deep in the jungles of Vietnam. After days of trekking through dense foliage, your team discovers an abandoned intelligence outpost that appears to have been hastily evacuated. As the team’s cryptanalyst, you’re tasked with investigating a small underground room containing what looks like a communication center. Among scattered papers and broken equipment, you find: A peculiar reference table (see attached image) with alphabetic grid patterns Scattered papers with two plaintext messages and three encrypted messages. Intelligence believes one of the three messages contains critical information about enemy operations. flag format: texsaw{FLAG}

We were provided with a file named MESSAGES.txt and an image named DIANA.tiff. The message file looked like this:

===== PLAINTEXT MESSAGES =====
-OPERATION BLUE EAGLE MOVING TO SECTOR FOUR STOP REQUEST EXTRACTION AT BLUE EAGLE
-AGENT SUNFLOWER COMPROMISED NEAR HANOI STOP ABORT MISSION COMPROMISED

===== ENCRYPTED MESSAGES =====
-RCPZURNPAQELEPJUJZEGAMVMXWVWCTBMHKNYEEAZVXQWVKGMRVWXDLCANHLGY
-FLPDBSBQIGBJECHMIOZGJMQONXJANFPQYQPWIIONYKNERKHIABLJTPTAOZMDGZUTAESK
-KDPRMZZKNBECTGTKMKQOWXKCHMVNDOPQXUWJJLECUCLBQKKVDXJNUEYFIDAGVIUG

However, a previous version of the file (which had a mistake) helped with deducing part of the encryption mechanism:

===== PLAINTEXT MESSAGES =====
-OPERATION BLUE EAGLE MOVING TO SECTOR FOUR STOP REQUEST EXTRACTION AT BLUE EAGLE
-AGENT SUNFLOWER COMPROMISED NEAR HANOI STOP ABORT MISSION COMPROMISED

===== ENCRYPTED MESSAGES =====
-RXPRB MYGLQHWPS VYXIIAWQJTV GXSE ADGUT LMIK TCAII FTLDTHG VYXIIAWQJTV
-FPLVOQLFPS XQNR XRAFP DAVPWZ OZ EOGGCS TFHT LCAK ICTMXGM XIHETRMBPG EE XQNR XRAFP
-MAT YETB HV PND LZXX IEC JQMM VNCTKLVGKDL TPGPXXN PHSXL PKRBIXW BG GSX AVRWVK

The first thing that caught my attention was the fact that the ciphertexts were of the same length as the plaintexts. This allowed me to tell apart the different ciphertext-plaintext pairs, something that was not possible with the second version of the file.

The image file was this:

A quick reverse image search revealed that this is an image of an example of the Diana One-Time Pad, a Cold War-era encryption scheme developed by the NSA. The Diana system uses a trigraph-based cipher, which applies a modular addition of characters (mod 26) to encode plaintext into ciphertext.

Understanding the Encryption Scheme

The Diana OTP encryption uses the following rule:

Trigraph Rule For each character pair (A, B): C = (A + B) mod 26

Where:

• A is the plaintext character
• B is the OTP key character
• C is the resulting ciphertext character

To decrypt, we reverse the operation: B = (C - A) mod 26

Strategy

1. Recover the OTP Key: Using one of the known plaintext and ciphertext pairs, we can reverse the trigraph rule to deduce the key letter-by-letter
2. Decrypt the target ciphertext: Once we have the key, we can decrypt the flag.

Implementation

def trigraph(a: str, b: str) -> str:
    """Encrypt using trigraph rule (A + B) % 26"""
    a_val = ord(a.upper()) - ord('A')
    b_val = ord(b.upper()) - ord('A')
    c_val = (a_val + b_val) % 26
    return chr(c_val + ord('A'))

def trigraph_reverse(c: str, a: str) -> str:
    """Recover B from C and A using (C - A) % 26"""
    c_val = ord(c.upper()) - ord('A')
    a_val = ord(a.upper()) - ord('A')
    b_val = (c_val - a_val + 26) % 26
    return chr(b_val + ord('A'))

def recover_key(known_plaintext: str, known_ciphertext: str) -> str:
    key = ""
    for p, c in zip(known_plaintext.replace(" ", ""), known_ciphertext.replace(" ", "")):
        key += trigraph_reverse(c, p)
    return key

def decrypt_with_key(ciphertext: str, key: str) -> str:
    ciphertext = ciphertext.replace(" ", "")
    plaintext = ""
    for i, c in enumerate(ciphertext):
        if i < len(key):
            plaintext += trigraph_reverse(c, key[i])
        else:
            plaintext += "?"
    return plaintext

# --- Known pair: plaintext and ciphertext 
known_plaintext =  "AGENTSUNFLOWERCOMPROMISEDNEARHANOISTOPABORTMISSIONCOMPROMISED"
known_ciphertext = "RCPZURNPAQELEPJUJZEGAMVMXWVWCTBMHKNYEEAZVXQWVKGMRVWXDLCANHLGY"

# --- Ciphertext to decode
target_ciphertext = "KDPRMZZKNBECTGTKMKQOWXKCHMVNDOPQXUWJJLECUCLBQKKVDXJNUEYFIDAGVUG".replace(" ", "")

# Step 1: recover the key
otp_key = recover_key(known_plaintext, known_ciphertext)

# Step 2: decode the unknown ciphertext
decoded = decrypt_with_key(target_ciphertext, otp_key)

# Output
print("Recovered OTP key (partial):", otp_key)
print("Decrypted message:", decoded)

The output of the code is:

Recovered OTP key (partial): RWLMBZTCVFQPAYHGXKNSOEDIUJRWLMBZTCVFQPAYHGXKNSOEDIUJRWLMBZTCV
Decrypted message: THEFLAGISWONTIMEPADWITHUNDERSCORESBETWEENWORDSWRAPPEDINTHEHEA??

And that is how we get the flag: texsaw{won_time_pad}

Brainstorming [Crypto]

Description: My friend is such a Joker, he has been sending me packets of data like the one attached, I can’t decrypt it! can you? flag format: texsaw{}

We were provided with a file named packet.txt whose contents were a long binary string.

You can download the file here.

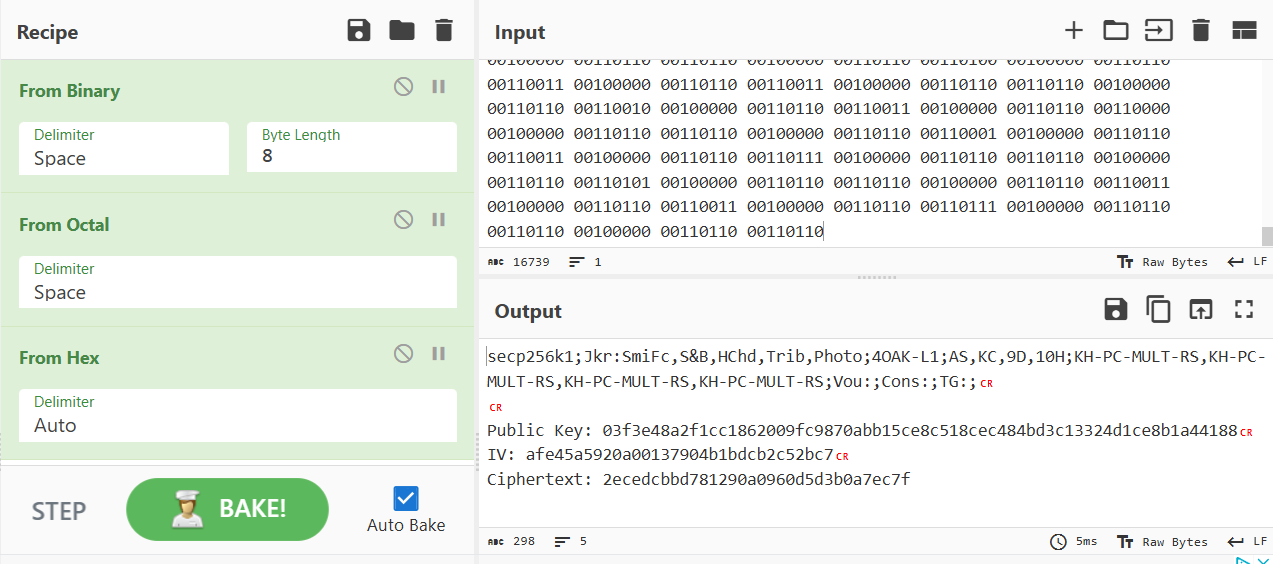
00110110 00110111 00100000 00110110 00110011 00100000 00110110 00110110 00100000 00110110 00110101 00100000 00110110 00110110 00100000 00110110 00110011 00100000 ...

Playing around in cyberchef, we find out we can decode that from binary, then octal, then hex. The result is the following:

We notice the following things:

• The first word refers to the SECP256k1 elliptic curve, which is used in Bitcoin and other cryptocurrencies.
• The rest of the “header” contains words that look like cards, for example Jkr (=Joker), AS (=Ace of Spades), 9D (=9 of Diamonds), etc.
• The last part of the message is a public key, an IV and a ciphertext.

Immediately we think of the following: There was some form of ECC encryption that was followed by AES, most likely in CBC mode.

Here was the real trick. Searching a bit on the internet, we discovered that many of the words in the header are actually cards from a game called “Balatro”. Balatro uses special cards like jokers and multipliers that give extra points to the player’s hand.

This leads to another thought: Maybe the score of the hand is important, possibly the private key for the ECC encryption. Using this site with the provided parameters included, we obtain a score of 483,662,483,600. Converting this number to hex yields us the private key 0x709c87d090, which we can quickly verify with the public key provided in the packet. We are on the right track.

Another thought would have been that the shared secret (the result of the ECC encryption) is used as the key for the AES encryption - more specifically the x-coordinate of the point. However, the admin got carried away and just ended up using the public key instead of the shared secret as the key for AES!!! Big curveball, still laughing about it with my teammates… Alternatively, we would have had a peer to exchange the secret with from whom we would obtain the shared secret.

To be able to use the secret - or rather public key here, we need to ensure that it is exactly 256 bits for AES to successfully decrypt the ciphertext. We can do this by hashing it with SHA256.

Finally, we can use the derived key to decrypt the ciphertext using AES in CBC mode. The IV is also provided in the packet.

from ecdsa import SECP256k1, SigningKey
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
import hashlib

# --- Given Data ---
card_score = 483662483600
public_key_hex = "03f3e48a2f1cc1862009fc9870abb15ce8c518cec484bd3c13324d1ce8b1a44188"
iv_hex = "afe45a5920a00137904b1bdcb2c52bc7"
ciphertext_hex = "2ecedcbbd781290a0960d5d3b0a7ec7f"

# --- Step 1: Derive ECC Private Key (k) and compute kG ---
# Create the signing key using the card score as the private key
sk = SigningKey.from_secret_exponent(card_score, curve=SECP256k1)

# Calculate the public key (kG), and get the x-coordinate
vk = sk.verifying_key
recomputed_point = vk.pubkey.point
x_bytes = int(recomputed_point.x()).to_bytes(32, byteorder='big')  # 32-byte x-coordinate for AES key
print("k:", card_score)
print("x-coordinate of kG (AES key):", x_bytes.hex())

# --- Step 2: hash the x-coordinate to derive a 256-bit AES key ---
aes_key = hashlib.sha256(x_bytes).digest()
print("AES key (SHA-256 of x-coordinate):", aes_key.hex())

# --- Step 3: AES Decryption using the derived AES key ---
iv = bytes.fromhex(iv_hex)
ciphertext = bytes.fromhex(ciphertext_hex)

cipher = AES.new(aes_key, AES.MODE_CBC, iv)

decrypted_data = cipher.decrypt(ciphertext)

try:
    plaintext = unpad(decrypted_data, AES.block_size)  # Try unpadding
except Exception as e:
    print("Padding error:", e)
    plaintext = decrypted_data  

print("Decrypted plaintext (utf-8):", plaintext.decode("utf-8"))

Output: texsaw{Baloopy}

This concludes the writeup for the challenges I solved during TexSAW CTF 2025. I hope you found it helpful and informative. If you have any questions or comments, feel free to reach out! Thanks for reading!